Das Federpendel – BM Physik

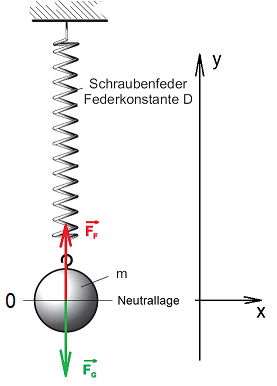
Eine Masse m, die an einer Schraubenfeder frei beweglich aufgehängt ist, wird als Federpendel bezeichnet. Einfachheitshalber soll die Masse nur vertikal, also entlang der Y-Achse sich auf und ab bewegen können, sämtliche seitlichen Bewegung werden wir nicht beachten.

Wenn die Masse $m$ an die Feder gehängt wird, dann streckt sich die Feder, bis die Federkraft $F_F$ gleich gross ist, wie die Gewichtskraft $F_G$ der Masse. Ohne weitere Einwirkung von Aussen, bleibt die Masse in dieser Position, der sogenannten Gleichgewichtslage. Man sagt auch, dass sich das Pendel in Neutrallage befindet.

Da die Feder durch die Federkonstante $D$ charakterisiert wird und die Federkraft $F_F$ proportional zur Auslenkung ist, berechnet sich die Federkraft als $F_F=D\cdot \Delta y$ .

Eine solche Schwingung, bei der $F_R \propto y$ wird auch als harmonisch bezeichnet. Harmonisch bedeutet, dass die Rückstellkraft $F_R$ proportional zur Auslenkung ist, also bei doppelter Auslenkung ist $F_R$ doppelt so gross und bei halber Auslenkung ist $F_R$ nur halb so gross.

Eine Masse von 7 kg wird an eine Feder mit D = 5 N/cm gehängt. Wie stark wir die Feder dabei verlängert? Antwort 1

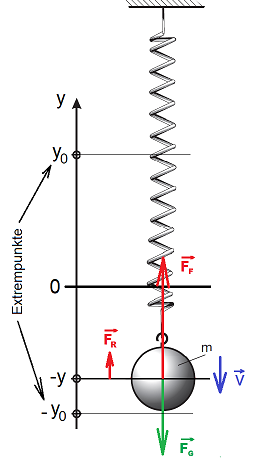
In Bild 2 ist zu sehen, wie sich die Kugel nach unten bewegt und bald den unteren Extrempunkt $-y_0$ erreichen wird. Betrachten wir die Kräfteverteilung, so stellen wir fest, dass die Federkraft $F_F$ grösser ist als die Gewichtskraft $F_G$ . Es resultiert also eine Kraft $F_R$ , die Rückstellkraft, welche der Bewegung der Kugel entgegengerichtet ist und somit abbremsend wirkt.

(1) $\begin{equation*}\vec{F}_R=\vec{F}_F+\vec{F}_G \notag\end{equation*}$

Die Rückstellkraft wird bis zum Umkehrpunkt weiter anwachsen und das Abbremsen noch verstärken. Beim Erreichen des Umkehrpunktes wird $F_R$ zur beschleunigenden Kraft. Dadurch beschleunigt die Kugel wieder nach oben und erreicht nach einer gewissen Zeit die Gleichgewichtslage, wo sie die maximale Geschwindigkeit hat. Die Rückstellkraft hat auf dem Weg von $-y_0$ bis 0 abgenommen und verschwindet in der Gleichgewichtslage ganz. Anschliessend findet der gleiche Prozess oberhalb der 0-Achse statt. Diesmal zeigt aber $F_R$ nach unten, da $F_G$ grösser ist als $F_F$ .

Bei welchen Punkten ist die Rückstellkraft $F_R$ am grössten und wo verschwindet sie? Antwort 2

Wie lange dauert es, bis die Kugel einmal eine ganze Pendelbewegung gemach hat? Eine ganze Pendelbewegung bedeutet, dass die Kugel wieder, von der gleichen Seite kommend, an einer bestimmten Stelle vorbeifliegt, z.B. die 0-Achse. Die Herleitung dieser Zeit, man spricht von der Periodendauer $T$ , übersteigt leider unsere mathematischen Fähigkeiten und daher müssen wir das Resultat dieser Berechnung einfach zur Kenntnis nehmen:

$\begin{aligned}T&=2\pi\cdot\sqrt[]{\frac{m}{D}}\quad[s]\end{aligned}$

Die Periodendauer $T$ hängt von der Masse $m$ und der Federkonstanten $D$ ab, jedoch nicht, wie stark die Kugel zu Beginn ausgelenkt wird.

Mit der Beziehung: $f = \frac{1}{T}$ kann auch die Frequenz der Schwingung berechnet werden:

$\begin{aligned}f&=\frac{1}{2\pi}\cdot\sqrt[]{\frac{D}{m}}\quad[s^{-1}]\end{aligned}$

Ein Federpendel mit einer Masse von 15 kg macht in 12 s drei volle Perioden. Welche Federkonstante muss die Feder dabei haben? Antwort 3

Die Bewegung der Schwingung kann mathematisch durch 3 Diagramme dargestellt werden, so wie wir das bereits aus der Kinematik kennen. Da gibt es einmal das Weg-Zeit-Diagramm ( $y_0-t$ ), das Geschwindigkeit-Zeit-Diagramm ( $v-t$ ) und das Beschleunigung-Zeit-Diagramm ( $a-t$ ).

Sie finden die Berechnung der Diagramme im folgenden PDF-Dokument. Wenn Sie das PDF-Dokument nicht bearbeiten können, so können sie die im PDF gestellten Aufgaben auch in der Geogebra Umgebung S+W y-t Diagramm lösen. Hier erhalten Sie Hilfe zur Benutzung der Geogebra Umgebung. Beachten Sie ausserdem auch die Möglichkeit der Simulation des Federpendels:

Arbeitsblatt-SW-Diagramme als PDF online oder Herunterladen

Für ein besseres Verständnis besteht auch die Möglichkeit das Federpendel zu simulieren: Simulation Federpendel

Zurück zu Schwingungen und Wellen oder weiter zu den Energiebetrachtungen.