Kräfte am Hang – BM Physik

Befindet sich eine Masse auf einer schiefen Ebene, so gibt es mindestens 4 Kräfte, die für die Bewegung des Fahrzeuges beachtet werden müssen (siehe Bild 1). Die Kräfte greifen im Schwerpunkt der Masse (des Campers) an. Wie immer vernachlässigen wir die Ausdehnung der Masse. Ausserdem nehmen wir an, dass der Camper sich nicht bewegt, er steht also still ( $v = 0$ m/s). In diesem Fall zeigt die Reibkraft nach oben und verhindert so, dass der Wagen rückwärts rollen kann. Stellen Sie sich vor, die Handbremse sei angezogen. Würde der Camper nach oben fahren, dann müsste die Reibkraft natürlich nach hinten zeigen!

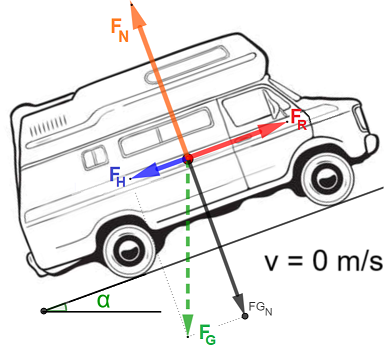
Die Gewichtskraft $F_G$ wird in die beiden Komponenten $F_{GN}$ und $F_H$ zerlegt:

Normalkomponente der Gewichtskraft: $\bf{F_{GN} = F_G \cdot \cos{ \alpha}}$
Hangabtriebskraft: $\bf{F_H = F_G \cdot \sin{ \alpha}}$

Sobald die Zerlegung in $F_{GN}$ und $F_H$ erfolgt ist, wird $F_G$ nicht mehr verwendet, was im Bild oben durch den gestrichelten Pfeil angedeutet wird. Der Wagen drückt jetzt mit der Kraft $F_{GN}$ auf die Unterlage. Die Unterlage reagiert daraufhin mit der Kraft $F_N$ (Normalkraft) zurück. Damit der Wagen auf der Unterlage bleibt, muss $F_N$ betragsmässig gleich gross sein, wie $F_ {GN}$ . Mathematisch sauber geschrieben:

$\lvert F_N \rvert = \lvert F_{GN} \rvert = \lvert F_G \cdot \cos{\alpha} \rvert$

Wäre dies nicht der Fall, dann würde sich der Wagen in die Richtung der grösseren der beiden Kräfte bewegen, also im Falle, wenn $F_{GN}$ grösser ist als $F_N$ : nach unten.

Warum muss man denn die Gewichtskraft überhaupt zerlegen? Vielleicht haben Sie sich diese Frage auch schon gestellt? Und was würden Sie antworten? Hier ist meine Antwort.

Im täglichen Gebrauch verwendet man dann nur noch die Normalkraft $F_N$ anstelle von $F_{GN}$ , welche am Hang, gemäss den Überlegungen von oben, wie folgt berechnet wird:

$F_N = F_G \cdot \cos{\alpha}$

Reibkraft am Hang

Beachten Sie, dass die Reibkraft gemäss Definition über die Normalkraft berechnet wird:

$F_R = \mu \cdot F_N$

und somit am Hang eine leicht andere Form hat, als in der Ebene:

$F_R = \mu \cdot F_N = \mu \cdot F_G \cdot \cos{\alpha}$

Dieser Unterschied in der Berechnung der Reibkraft am Hang gegenüber der Reibkraft in der Ebene ist sehr wichtig! Je steiler der Hang ist, desto kleiner wird die Normalkraft und damit die Reibkraft. Sehen Sie sich dazu auch die folgende Simulation an:

Hier können Sie sehen, wie sich die Beträge der Kräfte am Fahrzeug ändern, wenn der Steigungswinkel $\alpha$ ändert.

Zurück zur Startseite Dynamik